As 10 Equações Mais Importantes da História

Equação de Pitágoras (c^2 = a^2 + b^2)

A equação de Pitágoras, atribuída ao famoso matemático grego Pitágoras, descreve a relação entre os lados de um triângulo retângulo. Essa equação tem aplicações generalizadas na geometria, trigonometria e cálculo, e é fundamental para várias áreas da física e engenharia.

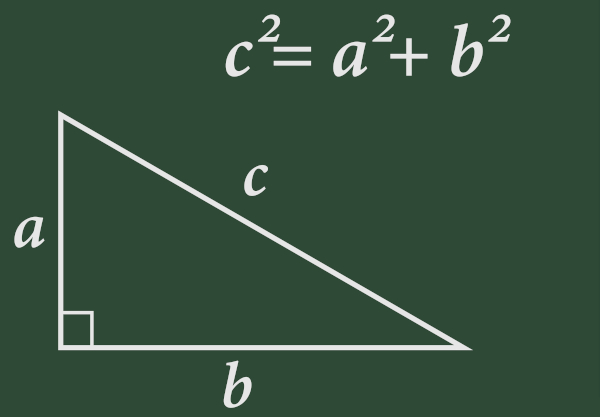
Lei da Gravitação Universal (F = G * (m1 * m2) / r^2)

A lei da gravitação universal, formulada por Isaac Newton, descreve a força de atração entre duas massas. Essa equação é essencial para o estudo da física e da astronomia, fornecendo uma base teórica para a compreensão do movimento dos planetas, estrelas e outros corpos celestes.

Equações de Maxwell (Equações de Maxwell do Eletromagnetismo)

As equações de Maxwell descrevem o comportamento do campo elétrico e do campo magnético e sua relação com as cargas elétricas e as correntes. Essas equações são fundamentais na teoria eletromagnética e na compreensão da eletricidade, magnetismo e propagação da luz.

Equação de Einstein (E = mc^2)

A famosa equação de Einstein, relacionando energia (E), massa (m) e a velocidade da luz ao quadrado (c^2), revolucionou a física com a teoria da relatividade. Essa equação estabelece a equivalência entre energia e massa, abrindo caminho para uma compreensão mais profunda da energia nuclear e das bombas atômicas.

Equações de Navier-Stokes (Equações do Movimento de Fluidos)

As equações de Navier-Stokes descrevem o movimento de fluidos, incluindo líquidos e gases. Essas equações são cruciais para a aerodinâmica, hidrodinâmica e engenharia de fluidos, sendo amplamente aplicadas em projetos de aeronaves, carros, barcos e outras estruturas que interagem com fluidos.

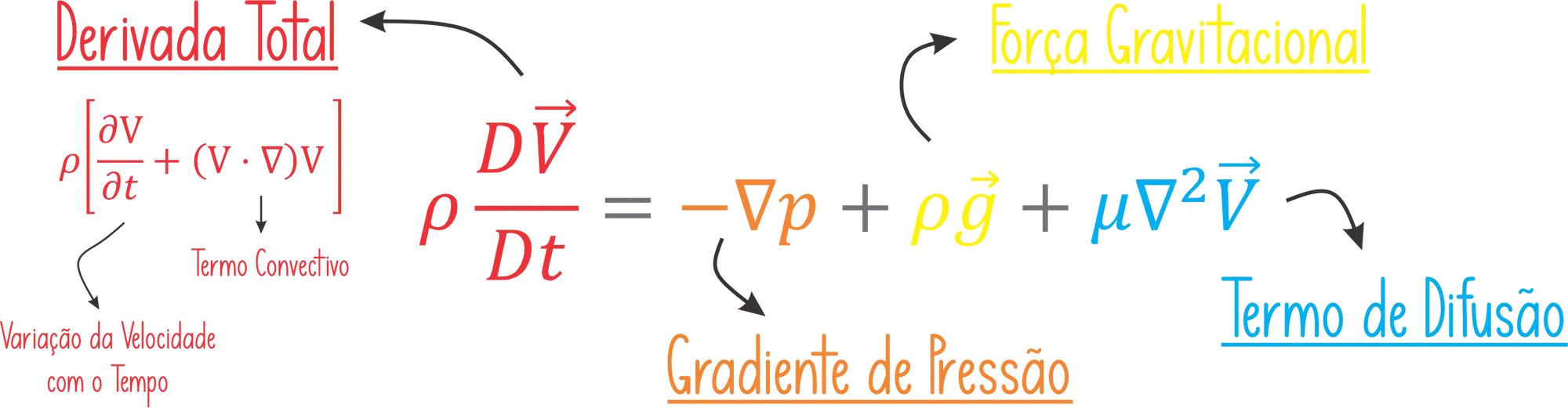
Equação de Schrödinger (Equação da Mecânica Quântica)

A equação de Schrödinger é uma equação fundamental na mecânica quântica, descrevendo a evolução temporal das funções de onda associadas a partículas subatômicas. Essa equação fornece uma base matemática para entender o comportamento dos elétrons, átomos e sistemas quânticos em geral.

Equações de Maxwell-Boltzmann (Distribuição Estatística de Velocidades)

As equações de Maxwell-Boltzmann descrevem a distribuição estatística das velocidades das partículas em um gás ideal. Essas equações são amplamente utilizadas na termodinâmica e na física estatística, permitindo a compreensão dos movimentos moleculares e das propriedades térmicas dos materiais.

Equação de Schroeder (Equação de Crescimento Populacional)

A equação de Schroeder é uma equação de diferenças finitas que modela o crescimento populacional. Essa equação tem aplicações em ecologia, economia e demografia, fornecendo uma base para entender as dinâmicas populacionais e o desenvolvimento sustentável.

Equações de Campo de Einstein (Equações da Relatividade Geral)

As equações de campo de Einstein são um conjunto de equações diferenciais que descrevem a teoria da gravidade, conhecida como relatividade geral. Essas equações têm sido fundamentais para o estudo do universo em larga escala, incluindo a cosmologia e a compreensão dos buracos negros e das ondas gravitacionais.

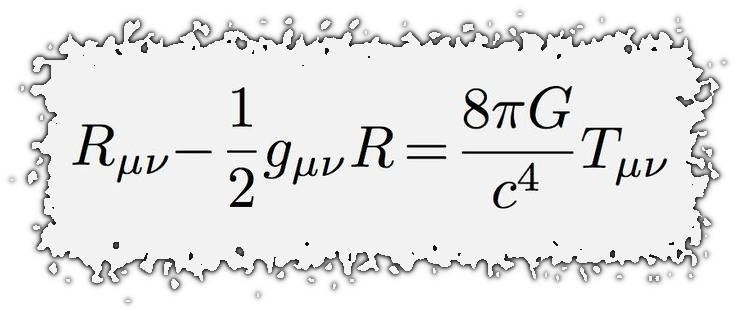
Equações de Black-Scholes (Modelo de Precificação de Opções)

As equações de Black-Scholes são um conjunto de equações diferenciais parciais que revolucionaram a teoria financeira, fornecendo uma maneira de precificar opções e derivativos financeiros. Essas equações têm implicações significativas na gestão de riscos, estratégias de investimento e tomada de decisões no mercado financeiro.

Conclusão

Essas 10 equações representam marcos importantes na história da matemática, da física, da engenharia e de outras áreas do conhecimento humano. Elas desempenharam um papel fundamental no avanço científico e tecnológico, moldando nossa compreensão do mundo e impulsionando a inovação. O estudo dessas equações não apenas revela a beleza e a elegância da matemática, mas também nos permite explorar e compreender melhor os fenômenos complexos que nos cercam.